CS360 Lab 5: Advanced Logistic Regression and Fairness Regularization

Due: Thursday, February 29 at 11:59pm

Overview

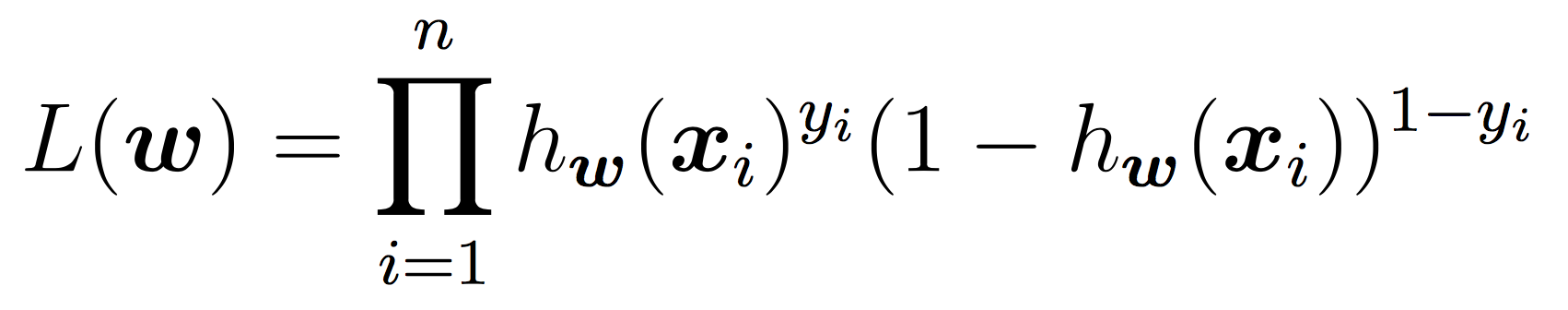
The goals of this week’s lab:

• Revisit stochastic gradient descent for Logistic Regression
• Augment our standard logistic regression algorithm with fairness regularization
• Consider hyperparameter tuning to increase performance

In this lab we will be analyzing the “Census Income” dataset, where the goal is to predict income from census attributes. We will think about this dataset in a slightly different context, where we are trying to ensure fairness based on sex. Race is also included in the dataset, but we will not consider this feature for now. Using our notation from class:

A = 1 (female, protected class) A = 0 (male, unprotected class) Y = 1 (income >= 50k) Y = 0 (income < 50k)

This lab may optionally be done in pairs (or you can work individually).

Getting Started

Find your git repo for this lab assignment the lab05 directory. You should have the following files:

• data - directory containing the train and test data.
• run_LR_fairness_regularizers.py - your main program executable for Logistic Regression.
• LogisticRegression.py - file for the LogisticRegression class (and/or functions).
• README.md - for analysis questions and lab feedback.

Usage and I/O

Usage

Your programs should take in the same command-line arguments as Lab 4 (feel free to reuse the argument parsing code), plus a parameter for the learning rate alpha and a parameter for the maximum number of SGD iterations t. For example:

python3 run_LR_fairness_regularizers.py -r data/adult/adult.data.cleaned.csv -e data/adult/adult.test.cleaned.csv -a <learning rate> -t <max iter>

Program Inputs

To simplify preprocessing, you may assume the following:

• I would recommend creating a function to parse the CSV file format. You are welcome to use pandas for this, which has a read_csv function. Save sex and the label separately, and omit race for now. So the features that we do want to consider for X are:

FEATURE_NAMES = ["age", "education-num", "capital-gain", "capital-gain", "capital-loss", "hours-per-week"]

• Make sure the user enters a positive alpha value (it should be type float) and a positive t value (of type int).

Program Outputs

• Your program should create six confusion matrix images (details below).

• The design of your solution is largely up to you. You don’t necessarily need to have a class, but you should use good top-down design principles so that your code is readable. Having functions for the cost, for SGD, for the logistic function, etc is a good idea.

Logistic Regression

You will implement the logistic regression task discussed in class for binary classification. This is similar to Lab 7 from CS260 and you’re welcome to reuse your code (all versions of CS260 did quite a bit with logistic regression, so feel free to use any of your code from CS260).

Step 1: Training without regularization (cost function)

To learn the weights, we will apply stochastic gradient descent as discussed in class until the cost function does not change in value (very much) for a given iteration. As a reminder, our cost function is the negative log of the likelihood function, which is:

Step 2: Stochastic Gradient Descent

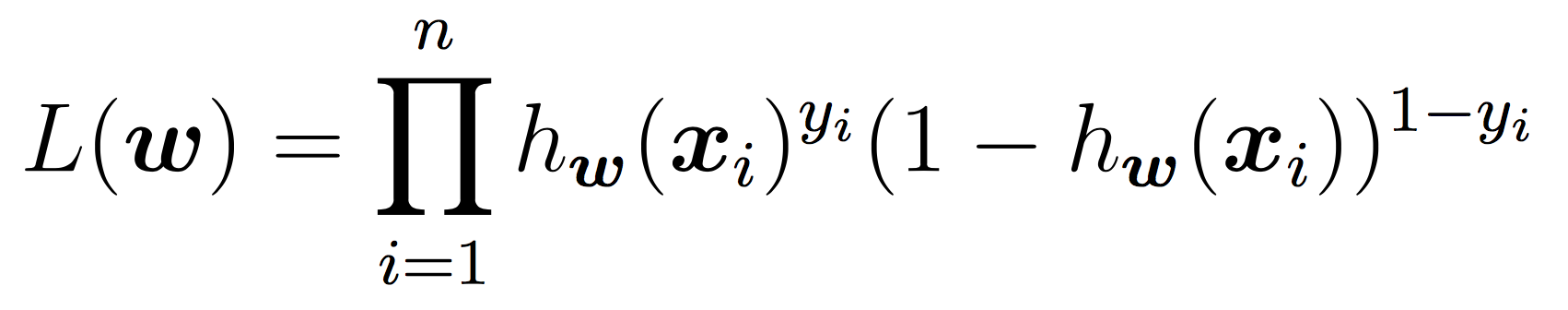
Our goal is to minimize the cost using SGD. Pseudocode:

initialize weights to 0's
while not converged:
    shuffle the training examples
    for each training example xi:
        calculate derivative of cost with respect to xi
        weights = weights - alpha*derivative
    compute and store current cost

The SGD updates for w term are:

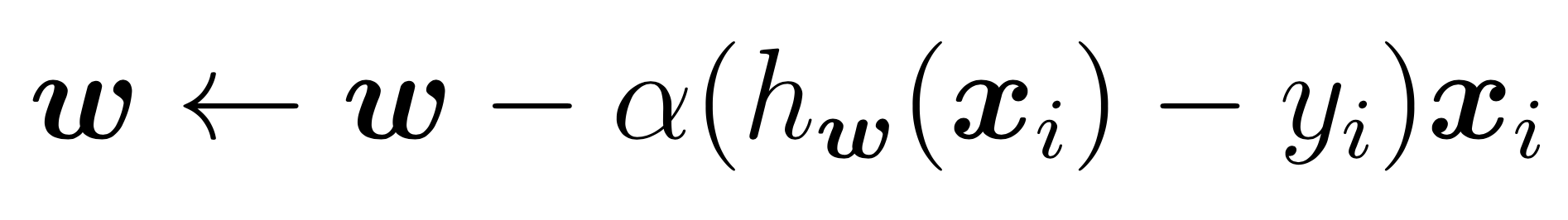
The hyper-parameter alpha (learning rate) should be sent as a parameter to your SGD and used in training. A few notes for the above:

• The stopping criteria should be a) a maximum of some number of iterations (your choice) OR b) the cost has changed by less some number between two iterations (your choice).

• Many of the operations above are on vectors. I recommend using numpy features such as dot product to make the code simple.

• Try to choose hyper-parameters that maximize the testing accuracy. A prediction function is provided in the starter code.

Step 3: adding in regularization

Now we will add in fairness regularization, following our discussion in class. For the cost and gradient descent functions, this will require two additional parameters:

Fairness regularization parameters:

• demographics should be a vector with the same shape as y and y_pred such that: 1 is the protected / not-privileged class 0 is the privileged class

• fair_reg_type takes options: None (for no fairness regularization), “demographic_parity” for a disparate impact focused regularizer, or “error_rate_balance” or any other string for an error rate balance regularizer

Make sure to change both the cost and the gradient in your algorithm.

Step 4: confusion matrices

To evaluate the impact of adding fairness regularization, we will create train 3 models:

• base: no fairness regularization
• DP fairness: demographic_parity option
• Error Rate fairness: error rate balance, just for the TPR case

Based on these three models, create 6 confusion matrices (i.e. the three models, but with the results separated by sex). Save these as PDF files in a figs folder.

In addition make sure to print (for each model)

• overall accuracy (based on the label)
• disparate impact score (demographic parity score)
• per-demographic group FPR and FNR

Analysis

(See README.md to answer these questions)

1. What do you notice about the 6 resulting confusion matrices and how they compare?

2. Which model version would you choose if your goal was to identify high earners for an IRS tax audit? Why?

3. What about if your goal was to determine what someone should be paid? Why?