CS360 Lab 4: Naive Bayes

Due: Tuesday, October 6 at 11:59pm

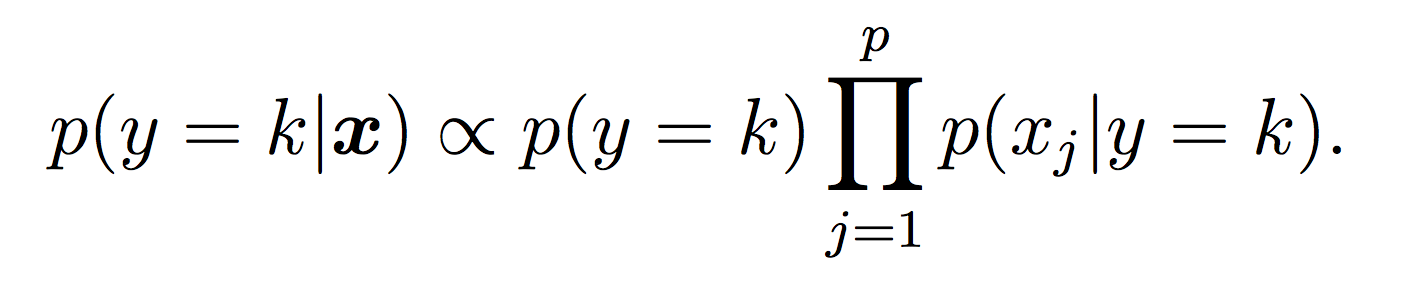
Grace period: will be collected Wednesday at midnight

Overview

The goals of this week’s lab:

• Understand the assumptions behind Naive Bayes
• Implement the Naive Bayes algorithm
• Practice multi-class prediction in a real-world setting

This week we will be analyzing the “zoo” dataset:

• Zoo data from Zoo Animal Classification by Kaggle. The class labels are:
  

Getting Started

Find your git repo for this lab assignment the lab04 directory. You should have the following files:

• input - directory containing train/test data sets. You may add additional data sets here.
• run_NB.py - your main program executable for Naive Bayes.
• NaiveBayes.py - file for the NaiveBayes class.
• README.md - for analysis questions and lab feedback.

Usage and I/O

Usage

Your programs should take in the same command-line arguments as Lab 2 (feel free to reuse this code). For example, to run Naive Bayes on the zoo example:

python3 run_NB.py -r input/zoo_train.arff -e input/zoo_test.arff

Program Inputs

To simplify preprocessing, you may assume the following:

• You may assume that all features are discrete (binary or multi-class) and unordered. You do not need to handle continuous features.

• Unlike Lab 2, prediction tasks can be multi-class. Think about how to modify the ARFF parser from Lab 2 to accommodate this.

• You can and should reuse as much as you can from Lab 2 (command-line arguments, ARFF file reading, Example class, Partition class, etc).

Program Outputs

• Your program should print a confusion matrix and accuracy of the result (see examples below).

• The design of your solution is largely up to you. I would recommend creating a NaiveBayes class, but you are not required to do this.

Naive Bayes

You will implement Naive Bayes as discussed in class. Your model will be capable of making multi-class predictions.

Model

Our Naive Bayes model for the class label k is:

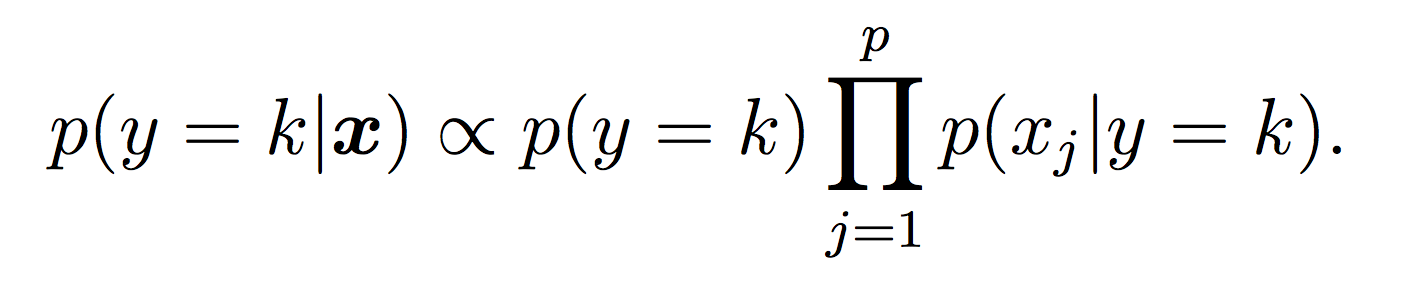
For this lab, all probabilities should be modeled using log probabilities to avoid underflow (depending on your system this might not absolutely be necessary, but it is good practice!) Note that when taking the log of a formula, all multiplications become additions and division become subtractions. First compute the log of the Naive Bayes model to make sure this makes sense.

Training

You will need to represent model parameters (θ’s) for each class probability p(y = k) and each class conditional probability p(x_j = v|y = k). This will require you to count the frequency of each event in your training data set. Use LaPlace estimates to avoid 0 counts. If you think about the formula carefully, you will note that we can implement our training phase using only integers to keep track of counts (and no division!) Each theta is just a normalized frequency where we count how many examples where x_j = v and the label is k and divide by the total number of examples where the label is k (plus the LaPlace estimate):

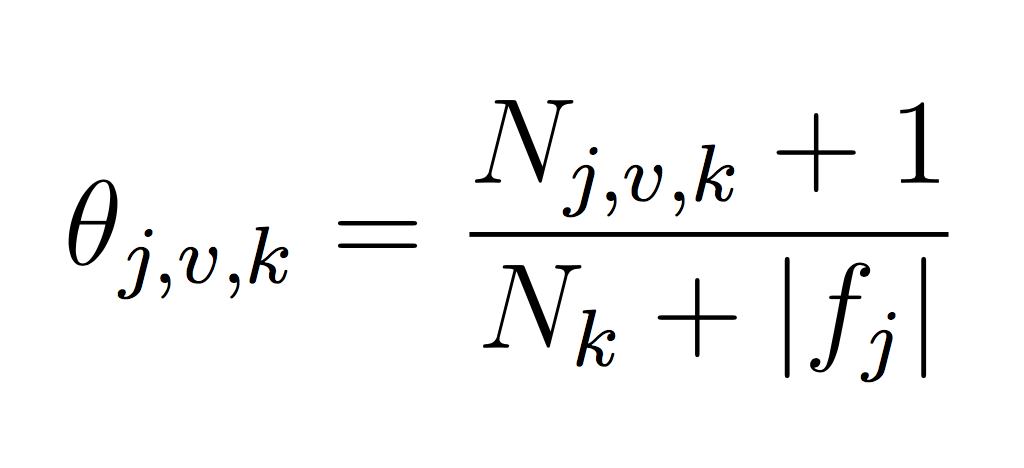
And similarly for the class probability estimates:

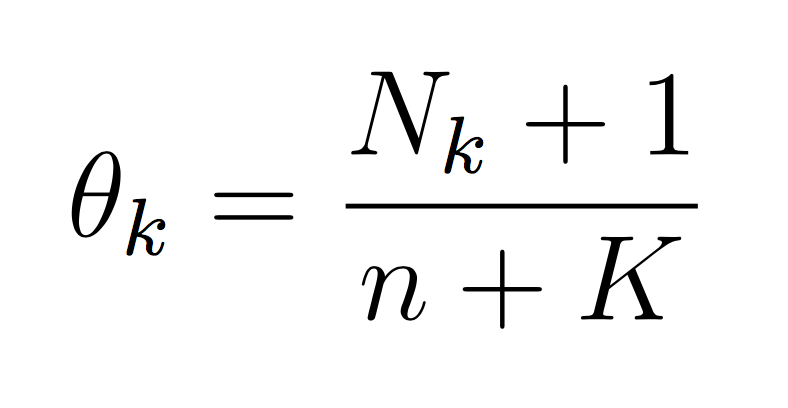
If we take the log then each theta becomes the difference between the two counts. The important point is that it is completely possible to train your Naive Bayes with only integers (the counts, N). You don’t need to calculate log scores until prediction time. This will make debugging (and training) much simpler.

Requirement: the model probabilities should be computed and stored in advance during training, not computed on the fly during testing (which results in duplicated computation).

Inference/Prediction

For this phase, simply calculate the probability of each class (using the model equations above) and choose the maximum probability:

Suggested steps

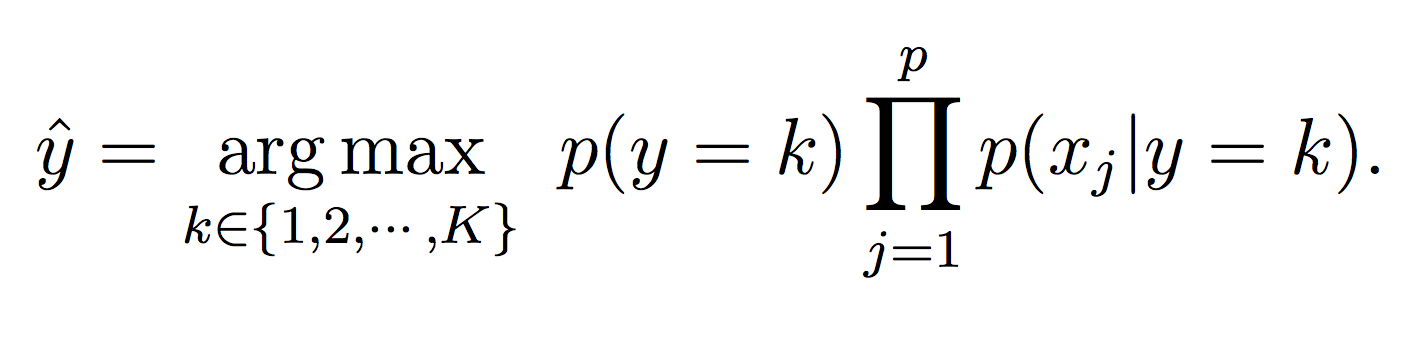
1. Copy over your util.py file from Lab 2 for editing. You can get rid of everything related to continuous features. You also need to change the label from {-1, 1} to {0,1,2,…,K-1}. Think about how to do this in the read_arff function. You can also copy over the Partition and Example classes and put them in util.py. I would recommend adding an argument K to the Partition constructor so you can keep track of the number of classes.

2. Test these modifications in run_NB.py by creating a similar main to Lab 2. Something like this:

def main():

    opts = util.parse_args()
    train_partition = util.read_arff(opts.train_filename)
    test_partition  = util.read_arff(opts.test_filename)

    # sanity check
    print("num train =", train_partition.n, ", num classes =", train_partition.K)
    print("num test  =", test_partition.n, ", num classes =", test_partition.K)

Here is what the output should be for the “zoo” dataset:

num train = 66 , num classes = 7
num test  = 35 , num classes = 7

3. Create a NaiveBayes class in NaiveBayes.py and do all the work of training (creating probability structures) in the constructor. Then in main, I should be able to do something like:

nb_model = NaiveBayes(train_partition)

It is okay to have your constructor call other methods from within the class.

4. Write a classify method within the NaiveBayes class and pass in each test example:

y_hat = nb_model.classify(example.features)

And compute the accuracy by comparing these predictions to the ground truth.

Example Output

• Tennis example:

$ python3 run_NB.py -r input/tennis_train.arff -e input/tennis_test.arff
Accuracy: 0.928571 (13 out of 14 correct)

  prediction
     0  1
   ------
 0|  4  1
 1|  0  9

Labels and Debugging Output

• Zoo example:

$ python3 run_NB.py -r input/zoo_train.arff -e input/zoo_test.arff
Accuracy: 0.857143 (30 out of 35 correct)

        prediction
     0  1  2  3  4  5  6
   ---------------------
 0| 13  0  0  1  0  0  0
 1|  0  7  0  0  0  0  0
 2|  0  1  0  0  1  0  0
 3|  0  0  0  4  0  0  0
 4|  0  0  0  0  1  0  0
 5|  0  0  0  0  0  3  0
 6|  0  0  0  0  0  2  2

Labels and Debugging Output

Extension (optional)

In these examples, our features were discrete. Devise a way to make Naive Bayes work with continuous features. Discuss your idea in the README and/or implement it (zip code is an example dataset to test this on).

Acknowledgements

Credit for this lab: modified from material created by Ameet Soni.