CS68 Lab 9: Principal Components Analysis

This lab is optional (not graded)

Overview and goals

The goals of this lab are:

• See how PCA can be applied to a real-world dataset to visualize population relationships
• Gain experience working with large datasets
• Understand the input to PCA and what it outputs
• Interpret the principal components in terms of evolutionary relationships

I have not made git repos for this lab, but if you would like one, send me an email and I'll make one for you (or for you and your partner).

Part 1: PCA on the Iris Flower Dataset

First we will apply PCA to a classic dataset of Iris flowers. This dataset is actually built-in to the package we will use: sklearn. To use this module, we will need to work in the virtual machine for our class:

source /usr/swat/bin/CS683env

Create a new python file pca_iris.py and import the necessary packages:

import numpy as np
import matplotlib.pyplot as plt

from sklearn import decomposition
from sklearn import datasets

The documentation for the PCA module can be found here.

The datasets module contains some example datasets, so we don't have to download them. To load the Iris dataset, use:

iris = datasets.load_iris()
X = iris.data
y = iris.target

X is our nxp matrix, where n=150 samples and p=4 features. Print X. The features in this case are not DNA data, but physical features of the flowers:

1. sepal length in cm
2. sepal width in cm
3. petal length in cm
4. petal width in cm

Our goal here is to use PCA to visualize this data (since we cannot view the points in 4D!) Through the process of visualization, we'll see if our data can be clustered based on the features above.

Now print y. These are the labels of each sample (subspecies of flower in this case). They are called:

• Iris Setosa (label 0)
• Iris Versicolour (label 1)
• Iris Virginica (label 2)

y is not used in PCA, it is only used afterward to visualize any clustering apparent in the results.

Run PCA

Using the PCA documentation, create an instance of PCA with 2 components, then "fit" it using only X. Then use the transform method to transform the features (X) into 2D. (3 lines of code!)

Plot the results

Now we will use matplotlib to plot the results in 2D, as a scatter plot. The scatter function takes in a list of x-coordinates, a list of y-coordinates, and a list of colors for each point. Here the two axes are PC1 and PC2, and the points to plot are formed from the first and second columns of the transformed data.

plt.scatter(x_coordinates, y_coordinates, c=colors) # example

First plot without the colors to see what you get. Then create a color dictionary that maps each label to a chosen color. Some colors have 1-letter abbreviations.

• 'b' - blue
• 'g' - green
• 'r' - red
• 'c' - cyan
• 'm' - magenta
• 'y' - yellow
• 'k' - black
• 'w' - white

After creating a color dictionary, use it to create a list of colors for all the points, then pass that in to your scatter method.

Legends are often created automatically in matplotlib, but for a scatter plot it's a bit more difficult. We'll actually create more plotting objects with no points, and then use these for our legend. Consider the code below. For each color, we're creating a null-plot (the 'o' means use circles for plotting). Then we're mapping these null objects to names of the flowers (create a list of names for each class).

# create legend
leg_objects = []
for i in range(3):
    circle, = plt.plot([], color_dict[i] + 'o')
    leg_objects.append(circle)
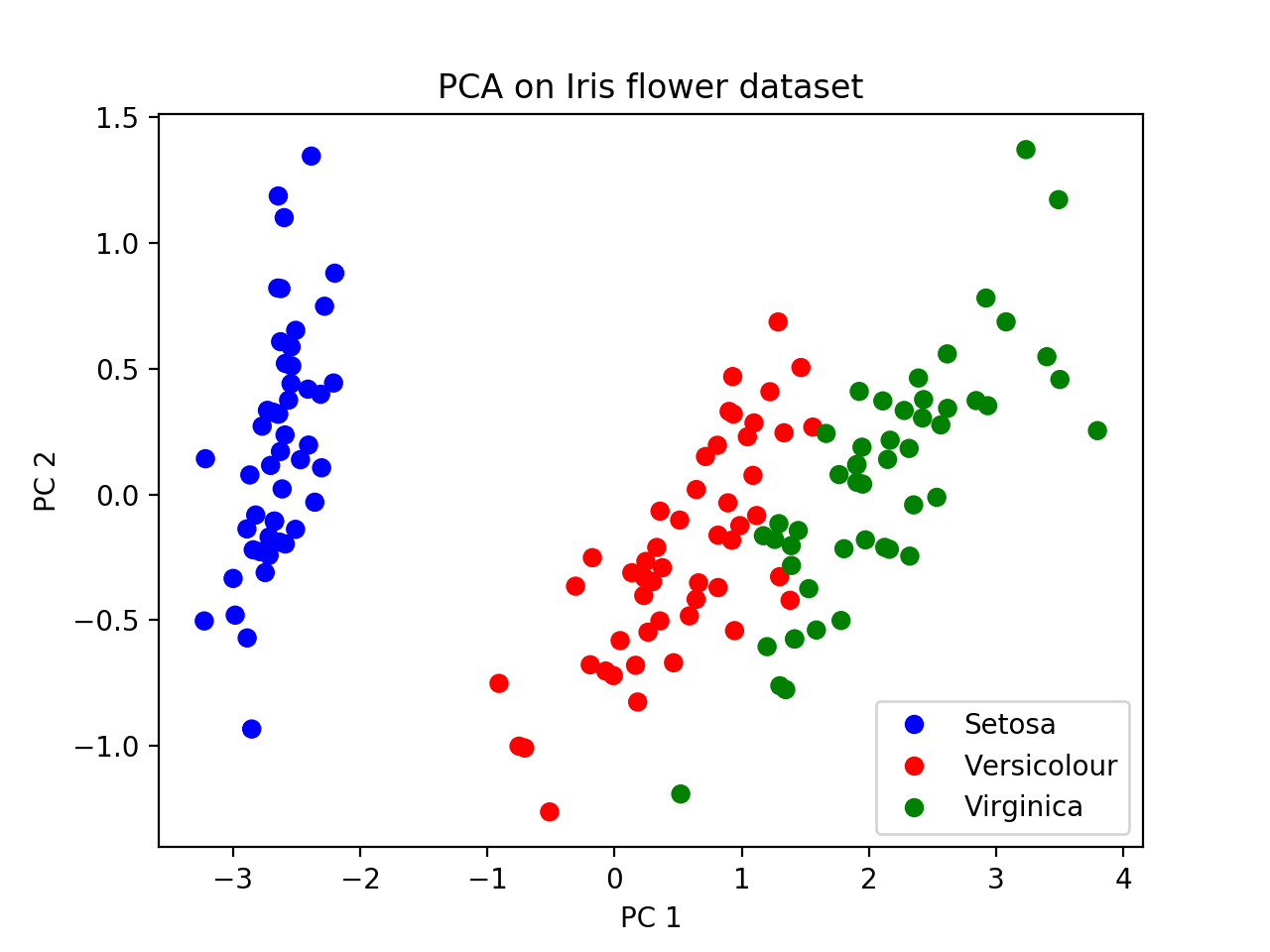
plt.legend(leg_objects,names)

At the end, you should get a picture like this. We can see that Setosa is further away from the other two subspecies with respect to PC1, suggesting that a tree relating these groups would have Versicolour and Virginica joining together first (i.e. most recently), and then finding a common ancestor with Setosa more anciently. This is the "genealogical interpretation of PCA".

Part 2: PCA on human data

Now we will apply PCA to human data, in the file:

/home/smathieson/public/cs68/1000g/ALL.chr2_start.vcf

This file contains about 10% of chromosome 2, for all samples in the 1000 genomes project Phase 3. It is 6.0Gb and contains about 600,000 SNPs. We will also make use of the file that maps each individual sample to its "super-population" (AFR, AMR, EAS, EUR, and SAS; see Lab 7 for more details).

/home/smathieson/public/cs68/1000g/igsr_samples.tsv

The starter code pca_human.py contains a VCF file parser which takes in the following arguments:

def parse_vcf(filename, sample_dict, n, p):

You should experiment with n (number of samples), and p (number of SNPs). These are also command line arguments to the script:

python3 pca_human.py -v home/smathieson/public/cs68/1000g/ALL.chr2_start.vcf
   -s /home/smathieson/public/cs68/1000g/igsr_samples.tsv -n 20 -p 1000 -o 1000genomes.pdf

The -o option is for the output file. First, create a sample_dict which maps each sample to its super-population (use the igsr_samples.tsv file, which is tab-separated).

Pass this into the VCF parser, which will return a list of super population names as well as the matrix X which is nxp. Then run PCA on this matrix using a similar method to the Iris dataset.

Finally, plot PC1 and PC2 as before, using the 1000 genomes color-coding for each super population. Keep experimenting with different values for n and p - try to use the largest numbers you can, but make sure plotting is working first since this can take a long time to run.

Analysis & Extension questions

1. What fraction of the variance is explained by the first PC? By the second? (Hint: see PCA documentation)

2. What genealogical relationships can we infer from PC1 and PC2?

3. Plot PC3 and PC4 on a separate plot. What genealogical relationships can we infer from these PCs?