CSC 212: Programming with Data Structures
Lab 11: Recursion
Due: Thursday, April 21, 11:59pm
A Fractal Dragon
For this lab, you will write a program that draws a shape called a fractal dragon. This is a linear fractal that connects two points. A particular dragon can be identified by a number corresponding to its complexity, called its rank or order. The order-0 and order-1 dragons are shown below.
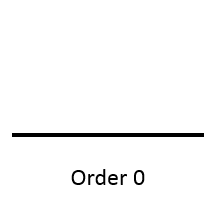
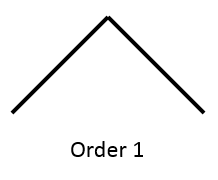
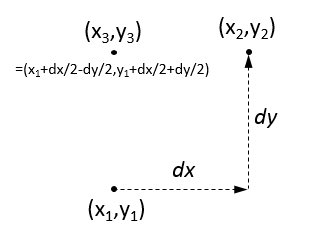
For order k > 1, the dragon is defined recursively. Consider the diagram below:
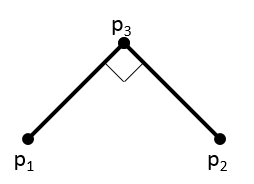
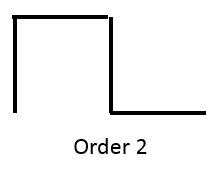
The order k dragon between p1 and p2 consists of two order k-1 dragons, one between points p1 and p3 and the other between points p2 and p3. Thus the order-2 dragon looks like the image below. Note how each of the line segments in the order-1 dragon has been replaced by two shorter segments at a 90 degree angle; each of these is an order-1 dragon. The order-1 dragon itself is composed of two order-0 dragons.
Given points p1 and p2, point p3 may be found through vector computations. Consider the vector p1p2 = (dx,dy). The perpendicular vector is (-dy,dx). Point p3 is thus p1+(dx/2-dy/2,dx/2+dy/2).
Coding the Dragon
A fractal dragon of order k can be displayed using a recursive program. Starting with this initial file, your job is to make it happen. (Note: this code combines the JDragon component with some static code that opens a GUI window to display into; this is not the best style under normal circumstances but it is convenient for labs because everything is in one file. Also note that your dragon will appear upside-down because the y-axis of the graphics plane is inverted.)
When you have your program running, it is interesting to try to predict what will happen if you (temporarily) comment out one or the other of the two recursive calls. Make a prediction in your head and test it out. This is a good test of whether you truly understand recursion.
Make sure to test your method with a variety of ranks (start with rank 0, 1, 2, etc).
To Submit
- JDragon.java, your completed version of the starter file given above.
- Dragon.png, a screenshot of a dragon of rank 18.