The goal of this homework is to practice working with transformation matrices. Credit: Joe O'Rourke

Matrix Transform, xkcd

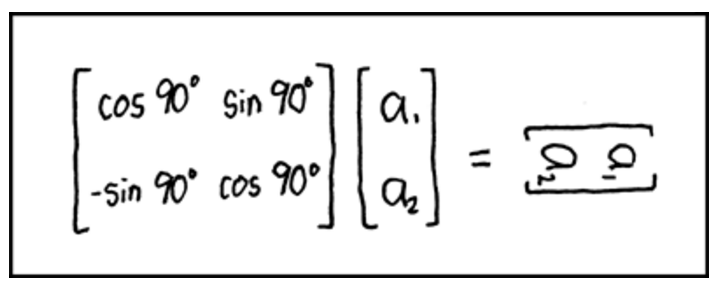
Answer the following Yes/No questions.

• If Yes, provide a mathematical proof with variables that covers all cases.

• If No, provide a concrete numerical counterexample and a corresponding picture.

Make sure you can multiply matrices by hand, even if you check your work with Mathematica, Matlab, or Wolfram Alpha.

1) Translations

Do 2D translations commute, i.e., is it always true that T₁T₂ = T₂T₁, where T₁ and T₂ are translation transformations?

2) Rotations

Do 2D rotations commute, i.e., is it always true that R₁R₂ = R₂R₁, where R₁ and R₂ are rotation transformations?

3) Translations and Rotations

Do 2D translations commute with rotations, i.e., is it always true that TR = RT, where T is a translation transformation and R is a rotation transformation?

4) Translations and Scalings

Do 2D translations commute with scalings, i.e., is it always true that TS = ST, where T is a translation transformation and S is a scaling transformation?

Submit

If you're interested in learning LaTeX, this might be a good opportunity to practice - you can start from the Transformations Source. Otherwise, write and draw your work, then scan it in as a PDF and submit on Moodle. If you absolutely cannot scan it, you can take pictures, but make sure they are submitted as a single document. Everyone must submit on Moodle.

Collaboration:

For this assignment, you are welcome to work together, but everyone should turn in their own work that they have written and understood. Please cite anyone you worked with (and any TAs) at the top of your assignment.

Extra Credit:

You may turn in either extra credit option from Homework 2 if you did not attempt it last week. Include an extra file called hw2_ec.html, with a comment at the top about what you did and if I need to do anything to run it.