CSC 240: Computer Graphics
Lab 9: Projection in OpenGL
Note: this lab will not be graded, but there will be some overlap with the 3D OpenGL homework.
- Download
lab9.py
and make sure you can run
python lab9.py
You should see a triangle that looks something like this (it's okay if the aspect ratio is not perfectly the same).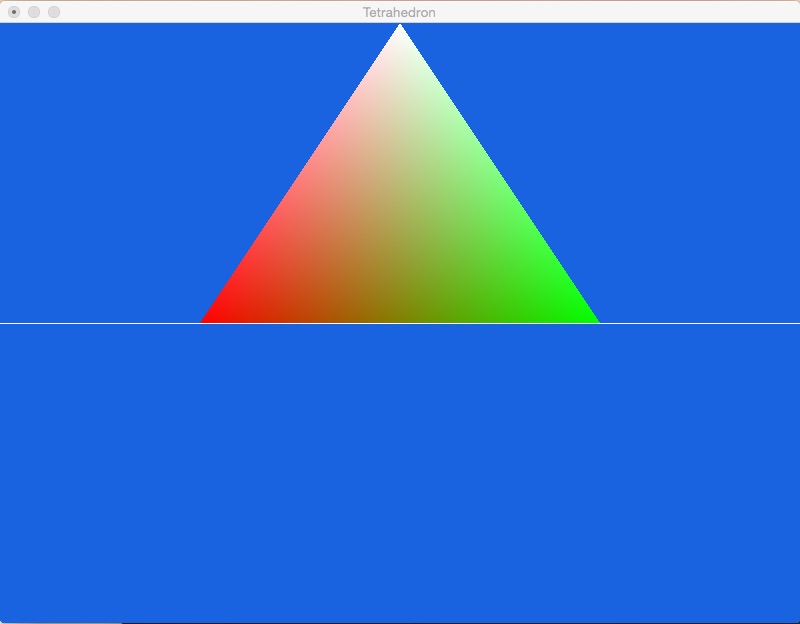
This first projection is orthographic. Find this in the code - what is the clipping window?
- From this viewpoint it looks like a triangle, but it is
actually a tetrahedron. Rotate the shape in the display() method so that you can see another
face, using:
glRotate(angle,x,y,z)
What angle should you use? What vector/axis should you rotate the shape around? It should look something like:
Rotate it again to see the last side face:
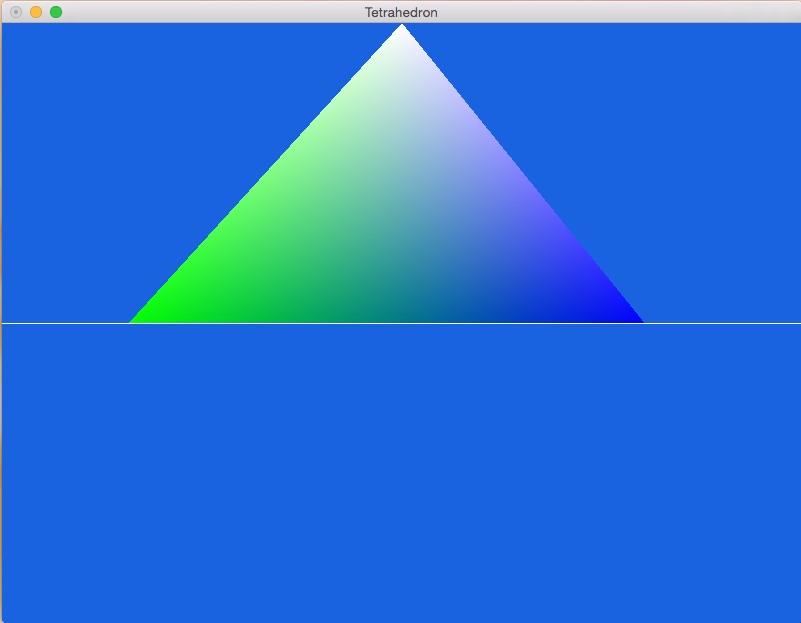
- Now change the projection from orthographic to perspective
(comment out the orthographic projection and uncomment the frustum
line). What are all the arguments for? Comment out the rotations you
made in the previous steps and see what happens. The tetrahedron
should disappear. Why is that? Use a transformation to bring the
shape back into view, similar to below:
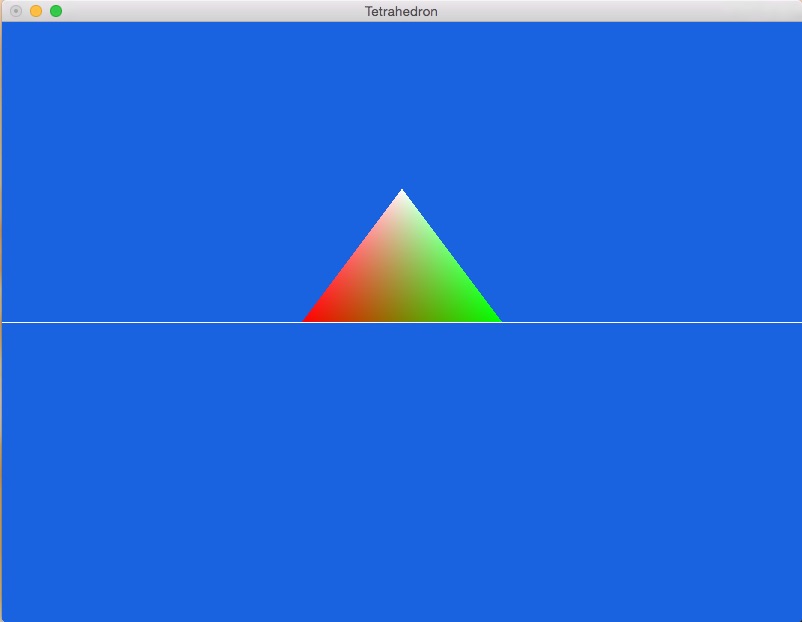
- Now rotate the shape to obtain a similar image to the one
below:
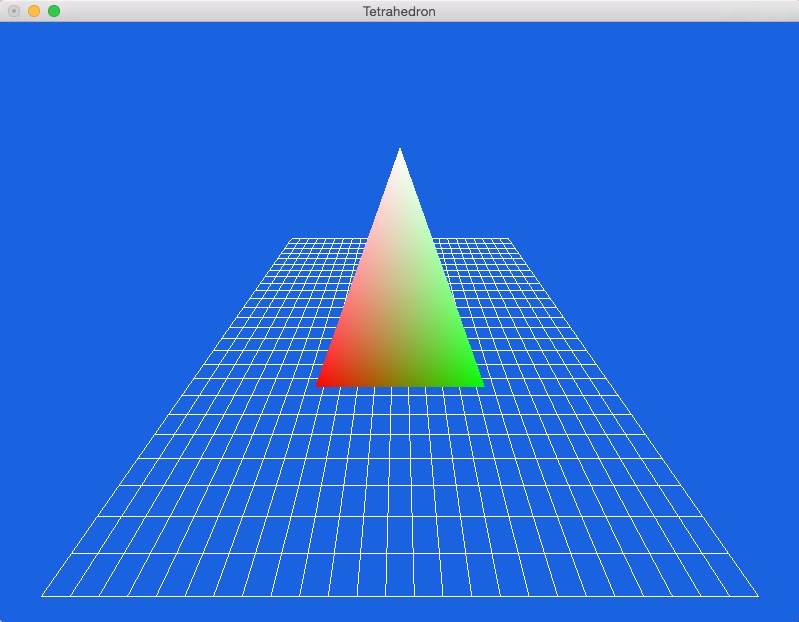
- Finally, rotate the shape again to obtain:
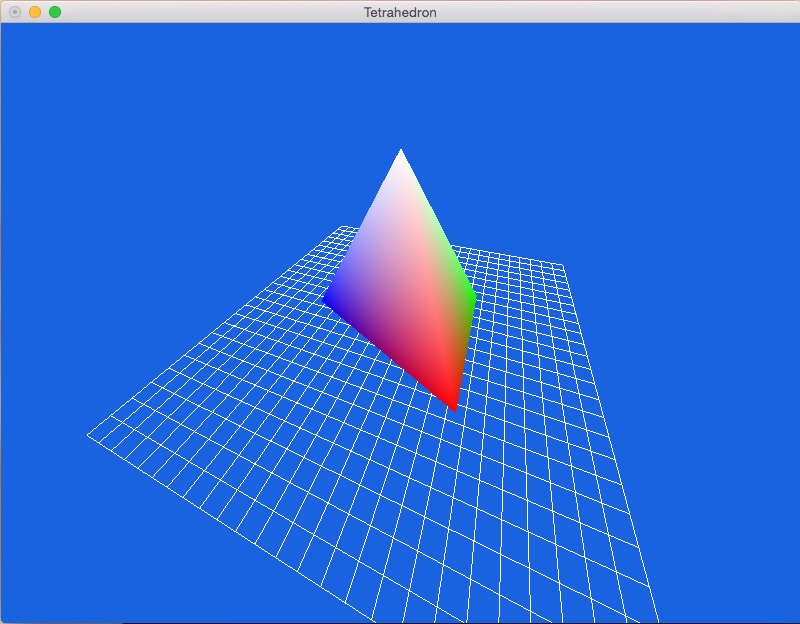
- Animate! Use transformation matrices (and the angle variable) to make it look like the grid and tetrahedron are moving in a circle, but in and out of the "page". So it looks like the shape is moving towards you, then to the right, then back into the screen, then left, etc. Example on the projector. What happens if the shape comes "too far" out of the page? What does this same animation look like in the orthographic projection?